定期的に数式いっぱいな記事を書かないと当ブログ、存在価値がないですからね(意味不明
※案の定色々と間違っていたので大幅加筆。
前回の更新が昨年ですので・・・あけましておめでとうございます!になるのでしょうか(汗
※案の定色々と間違っていたので大幅加筆。
前回の更新が昨年ですので・・・あけましておめでとうございます!になるのでしょうか(汗
そして、9期になってからはじめての更新になりますm(_ _)m
今期は佐竹家にてボチボチプレイをしているのですが。
なかなかにリアルが多忙でして、ようやく一息ついてきた今日この頃です。
そう言いながらも・・・しっかり合戦で無駄凸をしてサボっているくせに兵は貯まっていないという。。
今回は、昨日に実装されたスキル周りのアップデートのうち、
『スキル強化』での変更点と、現時点で分かっていることを整理してみたいなと思います。
部隊シミュレータの方の更新も、ゆっくり再起動!
DB更新やコメントを頂いている不具合の原因追及、特殊スキル対応等々は少々お待ちください^^
◆ □ ◆
まずは、特設ページよりそのまま抜粋。
- 強化合成の生贄にするカードのレアリティとランクによって、効果が変化する。
- 生贄にするカードは1回の合成で10枚までセット可能で、LV10に達した場合は余ったカードは返ってくる。
- 合成結果には「成功」「大成功」「極成功」「天晴成功」の4種類がある。
この3つが要点のようですね。
次に、細かいデータを表にまとめていきます。
――――――――――――――――――
補足1: あやめや雪乃丞は「特」、兵右衛門は「極」、いくさぶる・にゃんは「天」に分類。
補足2: 武将のレベルは関係ありません。★1LV0でも★1LV20でも効果は同じです。
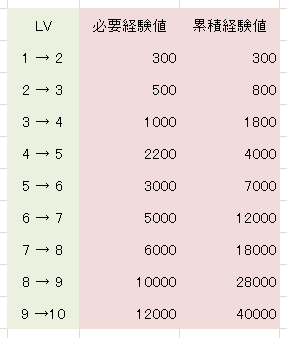
②各LVでの必要経験値
補足3: スキルのレアリティは関係なく、槍隊襲撃であろうが破軍星であろうが、全て一律。
LV1からLV10まで、合計で4万経験値が必要になるわけですね。
各レベル毎に区切りがある訳ではなく、例えばLV1スキルに☆4極カードを喰わせれば、
1回の合成でLV10になります。
各レベル毎に区切りがある訳ではなく、例えばLV1スキルに☆4極カードを喰わせれば、
1回の合成でLV10になります。
③合成結果によるボーナス補正
合成結果によって、生贄にセットされたカードの合計獲得経験値に補正がかかります。
「成功」 ・・・ 補正無し
「大成功」 ・・・ 1.2倍
「極成功」 ・・・ 1.5倍
「天晴成功」 ・・・ 2.0倍
補足4: 金50を使って合成した場合、「大成功」以上が保証されます。
――――――――――――――――――
おそらく、これであっている・・・と思われます。
◆ □ ◆
問題はここからですね。
どのように強化すれば、一番効率がいいのか?
幾つかのモデルケースから、一般化して考えてみます。
今回も、相変わらず説明が下手で・・・色々と散らばっていて、かつ様々な条件があって
非常に読み難いかと思います><;
記事を前後編に分けることも考えたのですが、きっとそうするとまた更新サボって中途半端になるのは過去からお察しですしね。。
結論だけ先書きします。
○●○●○●○●○●○●○●○●○●○●○●○●
LV1からLV10にするために必要な費用は、
◆銅銭合成オンリーの場合
○●○●○●○●○●○●○●○●○●○●○●○●
その根拠を知りたいという方、
間違い探しをしてくれる方は以下にお進みください。
ちなみに、上の大成功や極成功等の確率は適当に決めただけです><w ご注意を。
私は毎度毎度うっかりが多いですからね(苦笑
◆ □ ◆
ケース1) 金は使わず、素材調達は白くじのみ。全て銅銭、自前。合成は全てノーマル成功。
このケースが、理論上
「最低ナンボ使えばLV1からLV10にできるのか」という値になるわけですね。
白くじからの上排出率、序排出率をそれぞれp, 1-pとします。 (0 <= p <= 1.0)
特の排出率は・・・基本的に無視できるほど小さいということに><w
すると、白くじを1回引いて(=銅銭100につき)得られる獲得経験値をXとすると、
X = 300p + 100(1-p) = 100(2p+1)
ところがこれは、合成ボタンをポチる費用については考慮されていません。
なるべく合成ボタンを押す回数を減らすために、当然生贄はなるべく10枚セット。
白くじを10回引いて、1回合成をポチる。
(今回は端数は高々100銅銭の誤差として、考えていません・・・)
以下の話では、極力演算記号を減らすため、出てくる値が端数になったり、
合成回数が整数じゃなかったりするようになります。
どうしても確率が入ってしまうので「期待値」として考えていると察してもらえると幸いです。
とすると白くじ1回当たり、合成費用100のうちの1/10ずつを考慮していけばよいことになります。
『白くじを1回引いて得られる獲得経験値』は、実質的には
『銅銭110を支払って得られる獲得経験値』と等価であるとします。
これより、銅銭1当たりに得られる、
での獲得経験値の期待値をxとすると、
x = X/110 = 100(2p+1)/110 = (2p+1)/1.1
ここで、累計経験値をYだけ獲得するためには、『Y/x』だけの銅銭が必要になります。
これが最終的に求めたい、必要な銅銭額の期待値です。これをZとして、
Z = Y/x
LV1からLV10まで一気に上げる時のことを考えて、Y = 40000で固定します。
最初に、合成結果で一切大成功が起きない場合をまずは考えます。
大成功が起きると、その分だけ必要な銅銭は減りますので
「最低ナンボ使えばLV1からLV10にできるのか」という主旨からは外れますからね。
その場合、必要な銅銭額の期待値Zは、
Z = Y/x = 1.1Y/(2p+1) = 44000/(2p+1)
ここまでの条件で、更に白くじから序以外のカードが一枚も出なかった場合が、
考え得る最悪の銅銭消費量になります。上の式にp = 0を代入して、
白くじを連打して片っ端から10枚ずつ突っ込んで行けば、
最大でも44000銅銭を費やせば、どんなにくじ運が悪くてもLV10には到達する
ことが分かります。
・・・まぁ、こんなに遠回りしなくても自明なことです(苦笑
だって、序が1枚で100。4万経験値にするためには、序400枚。40回合成ボタンを押すのを加味すれば、100×(400+40) = 44000ですよね。。
ちなみに今期現時点での私の白くじ上排出率は、約25.3%。
大体4回に1回は上が出る、まぁまぁ標準的なぐらいなのではないでしょうか。
この想定だと、44000/(2*0.25+1) = 29334銅銭。端数切り上げ、およそ29400銅銭。
3万使えば、1つのスキルを市、ランクアップを使わずに自前でLV10にできます。
これは・・・私にしてみれば相当嬉しいんですが・・・!
これまでこの倍ぐらい使っていたことも平然とありましたからね><;;
運が無い人間、大部分のイクサーには救済処置であると考えます(笑
ケース2) ケース1に加えて、大成功する確率を考慮する
次に、合成結果のうち、確率qで大成功が発生する場合を考えます。
銅銭オンリーチャレンジなので、きっと極成功とか天晴成功なんてそれはそれはゴミみたいな確率、即ちほぼゼロであるとします。(という勝手な推測笑)
この辺りは、後々成功率が大まかに垣間見えてくると変更するかもしれません。
すると、ノーマル成功の確率は1-qとなります。(0 <= q <= 1.0)
上でも同じような事を言っています、
本来は端数処理をもう少し丁寧に考えるべきなのですが・・・
要は、確率qで、ノーマル成功時xの値が1.2倍になるということです。この場合のx'の値は、
上と同じようにして、
x' = q*1.2x + (1-q)x = (0.2q+1){(2p+1)/1.1}
ケース1と比べ、下線の部分『0.2q+1』が式に増えていますね。
これが、大成功を考慮することでxにかかる倍率です。
以降では、このような倍率を合成結果補正と呼ぶことにしてFと表すことにすると、
(今回の場合、F = 0.2q+1)
x' = Fx
と表現することができて、後々わかりやすくなります。
この場合に必要な銅銭額の期待値は、
Z = Y/x' = 1.1Y/{(0.2q+1)(2p+1)} = 44000/{(0.2q+1)(2p+1)}
例えば、大成功が20%の確率で引けたとして、q=0.2、p=0.25とすると、
44000/{(0.2*0.2+1)(2*0.25+1)} = 28205銅銭。端数切り上げ、およそ28300銅銭。
まあまあそんなものかなーという差ですねw
ケース3) ケース2までに加えて、ランクアップ素材を用いる場合を考慮。
ランクアップをすることで★が1つ増えると、獲得できる経験値が倍になります。
これは、特以上のカードだと主に視野に入ってくる選択肢かもしれません。
今回では簡単のため、ランクアップ素材をどれぐらいで市で買えば元が取れるのか、安いと言えるのかについて考えてみます。
Z = Y/xより、xがよりおおきくなると、必要な銅銭期待値Zがより小さくなるわけですが・・・
このxの値には、「白くじ10枚相当につき、合成費用1回分」が含まれているのでした。
この合成費用込みのxを使って比較をすると、
市からの購入素材にも合成費用を考慮しなければならないため面倒です。
銅銭1当たりに得られる、
z = X/100 = 2p+1
p=0.25とすると、
z = 2p+1 = 1.5。
このz = 1.5という値は、「大成功」以上を一切想定していない時の値なのが注意ですね。
より一般化すると、ケース2で定義した合成結果補正Fを使って、
z' = Fz
となるようなz'が一般には考えられます。
市から買ってきた素材の銅銭1当たりの獲得経験値の期待値ZEは、
ZE = 『素材の基本経験値E×合成結果補正F』/『素材落札額e-合成回数減による圧縮効果』
と考えます。
素材カードが白くじ武将何枚分の獲得経験値を持っているのかは、
EF/X = EF/(100z') = EF/(100Fz) = E/(100z) = E/150
となるので、合成回数減による圧縮効果の部分は、
{(EF/X)/10}*100 = {(E/150)/10}*100 = E/15
例えば、☆2特(獲得経験値3600)を銅銭2500で買った場合は、3600/15 = 240。
(白くじ武将24枚分の経験値があるので、合成回数2.4回減らせると考える。)
よって、『E/e = V』と置いて(Vの値は、購入素材の銅銭1当たりの基本獲得経験値)
ZE = (EF)/(e-E/15) = F(E/e)/{1-(E/e)/15} = FV/(1-V/15) = FVz/(z-0.1V)
で、問題はこのZEとやらとz'を比較して、
『ZE > z'』を満たすときには、購入が得であったと言えるわけです。つまり、
ZE/z' = V/(z-0.1V) >= 1 ⇔ V >= (10/11)z = 15/11(≒1.3636…)
この式が基本となります。
仮定では、合成結果補正Fがどうだ、z'がどうだという話をしましたが、
最後の式を見てみると、一定値になりましたね。
つまり、アバウトな余地はありますが、
購入した素材カードが、購入額の約1.37倍以上の獲得経験値を得られる場合は、
その素材カードはお買い得です!
一応、どれぐらいのお値段で購入すればこの条件を満たすのかをまとめたのが、
上で結論だけ書いていたところで貼った表になります。
完全に強化素材として全てのカードを見た場合、
この表よりも安く買えれば、まず間違いはないと思われます。
もっとも、これはpの値によって変動します。
要は、白くじの引き運にかなり依存している話、ということですね・・・
4枚に1枚は上カードが引ける自信がある人を基準としているという仮定があります。
例えば、上☆0を1枚市から買うとすると、
200銅銭出して購入すると、その1.5倍がちょうど300。これでようやく釣り合うことになります。
市でLV20カードを買って自力ランクアップをするとなると、
ランクアップ必要経費も当然含めなければなりません。
私は昨日、調子に乗って☆2極なんかを・・・
ヒャッハ―即落なんかしていたのですが、これはよくよく考えると割とおバカです^^;;
白くじを回す中で、ごく稀~に特が出る場合もありますし・・・
LV5止めでいいんだというカードには、上や序でちびちび強化の方が融通がききますからねw
額面だけで判断しきれない部分もあるにはあるわけですが。。
後述する金強化を使ったのですが、そこまでぐーんと特になっているわけではありません(笑
何故銅銭いっぱい持っているのか、なんていうのもまた後日のネタとして・・・w
無課金前提で行くと、結構シビア・・・ですよね・・・
データを理論的に分析すると、完全無課金万歳アプデではないように見えます。
(この私の考察があっているかは分かりませんがw)
ここぞというところで、レアの高い素材を使った時には金強化をするような微課金層が一番潤う気がします。私のような、月に実質ほぼデッキコストアップのみ、みたいな人間には、
削除金の分をこちらに回せばいいと考えると割と神アプデだと言えます!
ケース4) ケース2までに加えて、金合成を用いる場合。(常に金強化)
ここからが、金強化を用いるケースの考察になります。
金強化だと、必ず獲得経験値が1.2倍以上になるのは保証されます。
そのうち、確率rで極成功、確率sで天晴成功になるとします。
すると、大成功の確率は(1-r-s)になりますね。 (0 <= r, s <=1, 0 <= r+s <= 1)
あとは、ケース2と似たような計算になります。
市からの素材調達については、ケース5に分けるとして・・・
今回は、生贄調達は完全白くじオンリーとします。ややこしいので、全て金使用!
z' = (1-r-s)*1.2z + r*1.5z + s*2.0z
= (0.3r+0.8s+1.2)(2p+1)
x'と違ってz'なのは、金合成では合成費用は銅銭0だからですね。[ F = (0.3r+0.8s+1.2) ]
よって、この場合に必要な銅銭額の期待値は、
Z = Y/z' = Y/{(0.3r+0.8s+1.2)(2p+1)} = 40000/{(0.3r+0.8s+1.2)(2p+1)}
①「極成功」以上を一切考慮しない場合(F=1.2)
r=s=0とすると極成功以上は一切考慮しない想定になります。
この場合で、Z = 40000/{1.2(2p+1)} = 22222。端数切り上げ、およそ22300銅銭。
必要な金総額をMとすると、
必要な合成回数(白くじを引いた回数÷10)Nは、
N = (Y/X)/10 = Y/(10X)
Nを用いると、M = 50Nですね!
M = Y/(10X)*50 = {40000/(1000z)}*50 = (40/z)*50 = 2000/z
= 2000/{(0.3r+0.8s+1.2)(2p+1)}
と表すことができます。
これも、上と同様にr=s=0とすると、M = 2000/{1.2(2p+1)} = 1111。
端数切り上げ、およそ1150金。
②「極成功」以上を考慮する場合
どれぐらいの確率で極成功、天晴成功になるのかが何とも分からないので、
まぁ適当に・・・極成功10%、天晴成功3%ぐらいにしておきましょうかw
p=0.25, r=0.1, s=0.03を代入すると、
Z = 40000/{(0.3*0.1+0.8*0.03+1.2)(2*0.25+1)} = 21265銅銭。(F=1.254)
端数切り上げ、およそ21300銅銭。
①の時にでてきたMの式にそれぞれの値を代入して、M = 1063。
端数切り上げ、およそ1100金。
なんだかあまり①と変わらないですね・・・
極成功や天晴成功は、もう少し高い確率であってほしいですね(願望
ケース2(銅銭強化オンリー)で大成功を考慮した時と比較すると、
必要な銅銭額が28300-21300 = 7000銅銭減少。
その分金を余分に使っているので、金1あたりを銅銭換算額をmとすると、
m = 7000/1100 = 6.36程度
になります。金くじ1回を我慢して白連打、スキル強化に回すと、
(7000/1100)*600=約3818銅銭程度の節約になります。
金使用機能の中でも、かなりのコストパフォーマンスでしょうね・・・
こういう考察からも、金くじはもう少し優遇してあげてもいいと思いますね><;w
ちなみに、金合成オンリーでかつ、
白くじから一切上が出なく、さらに全てが大成功止まりでも、
100×1.2×334 = 40080。
銅銭33400と、金1700で理論上LV10に必ず到達します
ケース5) ケース4までに加えて、金強化と銅銭強化を混合。
上カード以上を生贄にする時のみ、金強化をする場合。
ここまで、白くじから25%で上は引けるんや!!! という仮定で書いてきました。
とすると、金強化はできるだけレアリティの高いカードばかりを集めてトライしたいですよね。
その方がぐいぐい伸びますから!
というわけで・・・全合成回数のうち、確率cだけ金強化を使う、ということにします。
残りの確率(1-c)はケチって銅銭強化、ということで。
文字が増えて、だんだんとこんがらがってきます・・・
ケース2とケース4の式を用いて、
x' = {(0.2q+1)(2p+1)}/1.1
z' = (0.3r+0.8s+1.2)(2p+1)
Z = Y/{cz' + (1-c)x'} = 40000/{c(0.3r+0.8s+1.2)(2p+1) + (1-c){(0.2q+1)(2p+1)}/1.1}
もうこれは変形するだけでごちゃごちゃになるのでこのまま・・・
c=p=0.25にすると、疑似的に上オンリー10枚を生贄にした時のみ、
金強化を使うという条件に近い値が出せます。
c=p=0.25, q=0.2, r=0.1, s=0.03をそれぞれ代入すると、Z=26077銅銭。
端数切り上げ、およそ26100銅銭。
使用した金の総額は、
M = c*50N = (2000c)/z = (2000c)/{(0.3r+0.8s+1.2)(2p+1)} = 265。
端数切り上げ、およそ300金。ケース2と比較してmを求めると、
m = (28300-26100)/300 = 7.33程度。
ケース4と比べて銅銭消費量は増えますが、金のコストパフォーマンスはよくなりましたね。
このあたりが最適解なのでしょうか。
ケース6) ケース5までに加えて、ランクアップ素材を用いる場合を考慮。
ケース5にて、当たり前ですが金は効果の高い生贄の時に集中して使うのがよろし、
というのが分かりました。
では、効果の高い生贄を市で調達してその時限定で金強化をする、
という戦略は当然の発想ですよね。
①常に金強化をする場合
ケース3とは異なり、合成回数が減ると、銅銭の節約ではなく金の節約になります。
よって、ZEは、
ZE = 『素材の基本経験値E×合成結果補正F』/『素材落札額e』 = EF/e = VF
ZE/z' = VF/(Fz) = V/z >= 1 ⇔ V >= z = 1.5
と随分と単純になります。
また、節約される金額は、ケース4②よりF = (0.3r+0.8s+1.2) = 1.254とすると、
{(E/X)/10}*50 = 5E/(100z') = E/(20Fz) = E/{20*1.254*1.5} = E/37.62 ≒ 0.02658…E
zは一定なので、Eが大きくなればなるほど節約金額が大きくなります。
今回の場合、素材カードの基本獲得経験値の約2.66%だけ節約になります。
以上をまとめると、
常に金強化をする場合、
購入した素材カードが、購入額の1.5倍以上の獲得経験値を得られる場合は、
その素材カードは(消費銅銭的にも)お買い得です!
節約される金の総額は、購入した素材カードの獲得経験値の約2.66%です。
②素材を購入した場合にのみ、金強化
銅銭節約、という意味では①よりもこちらでしょうか。
ここまで抽象的な話が多かったので、一度具体的な例を見て考えてみましょう。
ケース3で紹介した、私が☆2極を1万で買った場合だとどうなるでしょう?
1万払って12000の経験値を得るわけですから、V = 1.2。
また、ケース5より、金強化を行う時のF = 1.254。
ケース3から、購入した素材カードの銅銭1当たりの獲得経験値の期待値ZEは、
ZE = FVz/(z-0.1V) = 1.254*1.2*1.5/(1.5-0.1*1.2) = 1.6356…≒1.64
これと、銅銭強化を行う時(F=1.04)のz' = 1.04*1.5 = 1.56を比較して、
ZE > z'
つまり、割とギリギリプラス^^;;
・・・というのを、以下で数式にします。
金強化時、銅銭強化時の合成結果補正をそれぞれF, F'とすると、上と同じく
ZE = FVz/(z-0.1V)
として、ZE > F'zとなればいいので、
ZE/(F'z) = FV/{(z-0.1V)F'} >= 1 ⇔ FV >= F'(z-0.1V)
これを整理して、
V >= {F'/(F+0.1F')}z = {1.04/(1.254+0.1*1.04)}*1.5 = 1.1487…z≒1.149z
購入素材でのみ金強化をする場合、
購入した素材カードが、購入額の約1.15倍以上の獲得経験値を得られる場合は、
金消費と対価に、その素材カードはお買い得です!
これだと、結構割に合うケースが増えてきますね^^
具体的な境界値は、上のまとめで貼ってある表をご参照の事。
随分な長文かつ、意味不明な解析記事に付き合って頂きありがとうございましたm(_ _)m
合成結果によって、生贄にセットされたカードの合計獲得経験値に補正がかかります。
「成功」 ・・・ 補正無し
「大成功」 ・・・ 1.2倍
「極成功」 ・・・ 1.5倍
「天晴成功」 ・・・ 2.0倍
補足4: 金50を使って合成した場合、「大成功」以上が保証されます。
――――――――――――――――――
おそらく、これであっている・・・と思われます。
◆ □ ◆
問題はここからですね。
どのように強化すれば、一番効率がいいのか?
幾つかのモデルケースから、一般化して考えてみます。
今回も、相変わらず説明が下手で・・・色々と散らばっていて、かつ様々な条件があって
非常に読み難いかと思います><;
記事を前後編に分けることも考えたのですが、きっとそうするとまた更新サボって中途半端になるのは過去からお察しですしね。。
結論だけ先書きします。
○●○●○●○●○●○●○●○●○●○●○●○●
- 白くじから25%の確率で上カードは出る
- 銅銭合成において、大成功になる確率を20%とする
- 金合成において、極成功確率10%、天晴成功確率を3%とする
LV1からLV10にするために必要な費用は、
◆銅銭合成オンリーの場合
- どんなに運がなくても、理論上44000銅銭以下。
- 白くじオンリーで強化、大成功を一切考慮しない場合、かかる銅銭額は平均29400程度。
- 白くじオンリーで強化、大成功を考慮する場合、かかる銅銭額は平均28300程度。
◆金合成も用いる場合
- どんなに運がなくても、理論上33400銅銭&金1700消費以下。
- 白くじオンリーで強化、常に金強化で、極成功以上を一切考慮しない場合、
平均22300銅銭&金1150程度。 - 白くじオンリーで強化、常に金強化で、極成功以上を僅かながらも考慮する場合、
平均21300銅銭&金1100程度。 - 上のケースで、金強化を序生贄の時には使わないとすると、
平均26100銅銭&金300程度。当然だが、これが一番金効率がいい。
◆市から強化生贄を調達する場合
- 銅銭強化オンリーの場合、
購入した素材カードが、購入額の約1.37倍以上の獲得経験値を得られないと損。
以下の表中の数字以下の額で調達できればお得である。
- 金強化オンリーの場合、
購入した素材カードが、購入額の1.5倍以上の獲得経験値を得られないと損。
以下の表中の数字以下の額で調達できればお得である。
また、購入した素材カードの獲得経験値の約2.66%だけ金の節約になる。
表中の【】内の数字が、およその金節約可能額。
その根拠を知りたいという方、
間違い探しをしてくれる方は以下にお進みください。
ちなみに、上の大成功や極成功等の確率は適当に決めただけです><w ご注意を。
私は毎度毎度うっかりが多いですからね(苦笑
◆ □ ◆
ケース1) 金は使わず、素材調達は白くじのみ。全て銅銭、自前。合成は全てノーマル成功。
このケースが、理論上
「最低ナンボ使えばLV1からLV10にできるのか」という値になるわけですね。
白くじからの上排出率、序排出率をそれぞれp, 1-pとします。 (0 <= p <= 1.0)
特の排出率は・・・基本的に無視できるほど小さいということに><w
すると、白くじを1回引いて(=銅銭100につき)得られる獲得経験値をXとすると、
X = 300p + 100(1-p) = 100(2p+1)
ところがこれは、合成ボタンをポチる費用については考慮されていません。
なるべく合成ボタンを押す回数を減らすために、当然生贄はなるべく10枚セット。
白くじを10回引いて、1回合成をポチる。
(今回は端数は高々100銅銭の誤差として、考えていません・・・)
以下の話では、極力演算記号を減らすため、出てくる値が端数になったり、
合成回数が整数じゃなかったりするようになります。
どうしても確率が入ってしまうので「期待値」として考えていると察してもらえると幸いです。
とすると白くじ1回当たり、合成費用100のうちの1/10ずつを考慮していけばよいことになります。
『白くじを1回引いて得られる獲得経験値』は、実質的には
『銅銭110を支払って得られる獲得経験値』と等価であるとします。
これより、銅銭1当たりに得られる、
- 白くじ限定
- 強化合成、ノーマル成功オンリーとする
での獲得経験値の期待値をxとすると、
x = X/110 = 100(2p+1)/110 = (2p+1)/1.1
ここで、累計経験値をYだけ獲得するためには、『Y/x』だけの銅銭が必要になります。
これが最終的に求めたい、必要な銅銭額の期待値です。これをZとして、
Z = Y/x
LV1からLV10まで一気に上げる時のことを考えて、Y = 40000で固定します。
最初に、合成結果で一切大成功が起きない場合をまずは考えます。
大成功が起きると、その分だけ必要な銅銭は減りますので
「最低ナンボ使えばLV1からLV10にできるのか」という主旨からは外れますからね。
その場合、必要な銅銭額の期待値Zは、
Z = Y/x = 1.1Y/(2p+1) = 44000/(2p+1)
ここまでの条件で、更に白くじから序以外のカードが一枚も出なかった場合が、
考え得る最悪の銅銭消費量になります。上の式にp = 0を代入して、
白くじを連打して片っ端から10枚ずつ突っ込んで行けば、
最大でも44000銅銭を費やせば、どんなにくじ運が悪くてもLV10には到達する
ことが分かります。
・・・まぁ、こんなに遠回りしなくても自明なことです(苦笑
だって、序が1枚で100。4万経験値にするためには、序400枚。40回合成ボタンを押すのを加味すれば、100×(400+40) = 44000ですよね。。
ちなみに今期現時点での私の白くじ上排出率は、約25.3%。
大体4回に1回は上が出る、まぁまぁ標準的なぐらいなのではないでしょうか。
この想定だと、44000/(2*0.25+1) = 29334銅銭。端数切り上げ、およそ29400銅銭。
3万使えば、1つのスキルを市、ランクアップを使わずに自前でLV10にできます。
これは・・・私にしてみれば相当嬉しいんですが・・・!
これまでこの倍ぐらい使っていたことも平然とありましたからね><;;
運が無い人間、大部分のイクサーには救済処置であると考えます(笑
ケース2) ケース1に加えて、大成功する確率を考慮する
次に、合成結果のうち、確率qで大成功が発生する場合を考えます。
銅銭オンリーチャレンジなので、きっと極成功とか天晴成功なんてそれはそれはゴミみたいな確率、即ちほぼゼロであるとします。(という勝手な推測笑)
この辺りは、後々成功率が大まかに垣間見えてくると変更するかもしれません。
すると、ノーマル成功の確率は1-qとなります。(0 <= q <= 1.0)
上でも同じような事を言っています、
本来は端数処理をもう少し丁寧に考えるべきなのですが・・・
要は、確率qで、ノーマル成功時xの値が1.2倍になるということです。この場合のx'の値は、
上と同じようにして、
x' = q*1.2x + (1-q)x = (0.2q+1){(2p+1)/1.1}
ケース1と比べ、下線の部分『0.2q+1』が式に増えていますね。
これが、大成功を考慮することでxにかかる倍率です。
以降では、このような倍率を合成結果補正と呼ぶことにしてFと表すことにすると、
(今回の場合、F = 0.2q+1)
x' = Fx
と表現することができて、後々わかりやすくなります。
この場合に必要な銅銭額の期待値は、
Z = Y/x' = 1.1Y/{(0.2q+1)(2p+1)} = 44000/{(0.2q+1)(2p+1)}
例えば、大成功が20%の確率で引けたとして、q=0.2、p=0.25とすると、
44000/{(0.2*0.2+1)(2*0.25+1)} = 28205銅銭。端数切り上げ、およそ28300銅銭。
まあまあそんなものかなーという差ですねw
ケース3) ケース2までに加えて、ランクアップ素材を用いる場合を考慮。
ランクアップをすることで★が1つ増えると、獲得できる経験値が倍になります。
これは、特以上のカードだと主に視野に入ってくる選択肢かもしれません。
今回では簡単のため、ランクアップ素材をどれぐらいで市で買えば元が取れるのか、安いと言えるのかについて考えてみます。
Z = Y/xより、xがよりおおきくなると、必要な銅銭期待値Zがより小さくなるわけですが・・・
このxの値には、「白くじ10枚相当につき、合成費用1回分」が含まれているのでした。
この合成費用込みのxを使って比較をすると、
市からの購入素材にも合成費用を考慮しなければならないため面倒です。
銅銭1当たりに得られる、
- 合成費用は考えない
- 白くじ限定
- 強化合成、ノーマル成功オンリーとする
z = X/100 = 2p+1
p=0.25とすると、
z = 2p+1 = 1.5。
このz = 1.5という値は、「大成功」以上を一切想定していない時の値なのが注意ですね。
より一般化すると、ケース2で定義した合成結果補正Fを使って、
z' = Fz
となるようなz'が一般には考えられます。
市から買ってきた素材の銅銭1当たりの獲得経験値の期待値ZEは、
ZE = 『素材の基本経験値E×合成結果補正F』/『素材落札額e-合成回数減による圧縮効果』
と考えます。
素材カードが白くじ武将何枚分の獲得経験値を持っているのかは、
EF/X = EF/(100z') = EF/(100Fz) = E/(100z) = E/150
となるので、合成回数減による圧縮効果の部分は、
{(EF/X)/10}*100 = {(E/150)/10}*100 = E/15
例えば、☆2特(獲得経験値3600)を銅銭2500で買った場合は、3600/15 = 240。
(白くじ武将24枚分の経験値があるので、合成回数2.4回減らせると考える。)
よって、『E/e = V』と置いて(Vの値は、購入素材の銅銭1当たりの基本獲得経験値)
ZE = (EF)/(e-E/15) = F(E/e)/{1-(E/e)/15} = FV/(1-V/15) = FVz/(z-0.1V)
で、問題はこのZEとやらとz'を比較して、
『ZE > z'』を満たすときには、購入が得であったと言えるわけです。つまり、
ZE/z' = V/(z-0.1V) >= 1 ⇔ V >= (10/11)z = 15/11(≒1.3636…)
この式が基本となります。
仮定では、合成結果補正Fがどうだ、z'がどうだという話をしましたが、
最後の式を見てみると、一定値になりましたね。
つまり、アバウトな余地はありますが、
購入した素材カードが、購入額の約1.37倍以上の獲得経験値を得られる場合は、
その素材カードはお買い得です!
一応、どれぐらいのお値段で購入すればこの条件を満たすのかをまとめたのが、
上で結論だけ書いていたところで貼った表になります。
完全に強化素材として全てのカードを見た場合、
この表よりも安く買えれば、まず間違いはないと思われます。
もっとも、これはpの値によって変動します。
要は、白くじの引き運にかなり依存している話、ということですね・・・
4枚に1枚は上カードが引ける自信がある人を基準としているという仮定があります。
例えば、上☆0を1枚市から買うとすると、
200銅銭出して購入すると、その1.5倍がちょうど300。これでようやく釣り合うことになります。
市でLV20カードを買って自力ランクアップをするとなると、
ランクアップ必要経費も当然含めなければなりません。
私は昨日、調子に乗って☆2極なんかを・・・
ヒャッハ―即落なんかしていたのですが、これはよくよく考えると割とおバカです^^;;
白くじを回す中で、ごく稀~に特が出る場合もありますし・・・
LV5止めでいいんだというカードには、上や序でちびちび強化の方が融通がききますからねw
額面だけで判断しきれない部分もあるにはあるわけですが。。
後述する金強化を使ったのですが、そこまでぐーんと特になっているわけではありません(笑
何故銅銭いっぱい持っているのか、なんていうのもまた後日のネタとして・・・w
無課金前提で行くと、結構シビア・・・ですよね・・・
データを理論的に分析すると、完全無課金万歳アプデではないように見えます。
(この私の考察があっているかは分かりませんがw)
ここぞというところで、レアの高い素材を使った時には金強化をするような微課金層が一番潤う気がします。私のような、月に実質ほぼデッキコストアップのみ、みたいな人間には、
削除金の分をこちらに回せばいいと考えると割と神アプデだと言えます!
ケース4) ケース2までに加えて、金合成を用いる場合。(常に金強化)
ここからが、金強化を用いるケースの考察になります。
金強化だと、必ず獲得経験値が1.2倍以上になるのは保証されます。
そのうち、確率rで極成功、確率sで天晴成功になるとします。
すると、大成功の確率は(1-r-s)になりますね。 (0 <= r, s <=1, 0 <= r+s <= 1)
あとは、ケース2と似たような計算になります。
市からの素材調達については、ケース5に分けるとして・・・
今回は、生贄調達は完全白くじオンリーとします。ややこしいので、全て金使用!
z' = (1-r-s)*1.2z + r*1.5z + s*2.0z
= (0.3r+0.8s+1.2)(2p+1)
x'と違ってz'なのは、金合成では合成費用は銅銭0だからですね。[ F = (0.3r+0.8s+1.2) ]
よって、この場合に必要な銅銭額の期待値は、
Z = Y/z' = Y/{(0.3r+0.8s+1.2)(2p+1)} = 40000/{(0.3r+0.8s+1.2)(2p+1)}
①「極成功」以上を一切考慮しない場合(F=1.2)
r=s=0とすると極成功以上は一切考慮しない想定になります。
この場合で、Z = 40000/{1.2(2p+1)} = 22222。端数切り上げ、およそ22300銅銭。
必要な金総額をMとすると、
必要な合成回数(白くじを引いた回数÷10)Nは、
N = (Y/X)/10 = Y/(10X)
Nを用いると、M = 50Nですね!
M = Y/(10X)*50 = {40000/(1000z)}*50 = (40/z)*50 = 2000/z
= 2000/{(0.3r+0.8s+1.2)(2p+1)}
と表すことができます。
これも、上と同様にr=s=0とすると、M = 2000/{1.2(2p+1)} = 1111。
端数切り上げ、およそ1150金。
②「極成功」以上を考慮する場合
どれぐらいの確率で極成功、天晴成功になるのかが何とも分からないので、
まぁ適当に・・・極成功10%、天晴成功3%ぐらいにしておきましょうかw
p=0.25, r=0.1, s=0.03を代入すると、
Z = 40000/{(0.3*0.1+0.8*0.03+1.2)(2*0.25+1)} = 21265銅銭。(F=1.254)
端数切り上げ、およそ21300銅銭。
①の時にでてきたMの式にそれぞれの値を代入して、M = 1063。
端数切り上げ、およそ1100金。
なんだかあまり①と変わらないですね・・・
極成功や天晴成功は、もう少し高い確率であってほしいですね(願望
ケース2(銅銭強化オンリー)で大成功を考慮した時と比較すると、
必要な銅銭額が28300-21300 = 7000銅銭減少。
その分金を余分に使っているので、金1あたりを銅銭換算額をmとすると、
m = 7000/1100 = 6.36程度
になります。金くじ1回を我慢して白連打、スキル強化に回すと、
(7000/1100)*600=約3818銅銭程度の節約になります。
金使用機能の中でも、かなりのコストパフォーマンスでしょうね・・・
こういう考察からも、金くじはもう少し優遇してあげてもいいと思いますね><;w
ちなみに、金合成オンリーでかつ、
白くじから一切上が出なく、さらに全てが大成功止まりでも、
100×1.2×334 = 40080。
銅銭33400と、金1700で理論上LV10に必ず到達します
ケース5) ケース4までに加えて、金強化と銅銭強化を混合。
上カード以上を生贄にする時のみ、金強化をする場合。
ここまで、白くじから25%で上は引けるんや!!! という仮定で書いてきました。
とすると、金強化はできるだけレアリティの高いカードばかりを集めてトライしたいですよね。
その方がぐいぐい伸びますから!
というわけで・・・全合成回数のうち、確率cだけ金強化を使う、ということにします。
残りの確率(1-c)はケチって銅銭強化、ということで。
文字が増えて、だんだんとこんがらがってきます・・・
ケース2とケース4の式を用いて、
x' = {(0.2q+1)(2p+1)}/1.1
z' = (0.3r+0.8s+1.2)(2p+1)
Z = Y/{cz' + (1-c)x'} = 40000/{c(0.3r+0.8s+1.2)(2p+1) + (1-c){(0.2q+1)(2p+1)}/1.1}
もうこれは変形するだけでごちゃごちゃになるのでこのまま・・・
c=p=0.25にすると、疑似的に上オンリー10枚を生贄にした時のみ、
金強化を使うという条件に近い値が出せます。
c=p=0.25, q=0.2, r=0.1, s=0.03をそれぞれ代入すると、Z=26077銅銭。
端数切り上げ、およそ26100銅銭。
使用した金の総額は、
M = c*50N = (2000c)/z = (2000c)/{(0.3r+0.8s+1.2)(2p+1)} = 265。
端数切り上げ、およそ300金。ケース2と比較してmを求めると、
m = (28300-26100)/300 = 7.33程度。
ケース4と比べて銅銭消費量は増えますが、金のコストパフォーマンスはよくなりましたね。
このあたりが最適解なのでしょうか。
ケース6) ケース5までに加えて、ランクアップ素材を用いる場合を考慮。
ケース5にて、当たり前ですが金は効果の高い生贄の時に集中して使うのがよろし、
というのが分かりました。
では、効果の高い生贄を市で調達してその時限定で金強化をする、
という戦略は当然の発想ですよね。
①常に金強化をする場合
ケース3とは異なり、合成回数が減ると、銅銭の節約ではなく金の節約になります。
よって、ZEは、
ZE = 『素材の基本経験値E×合成結果補正F』/『素材落札額e』 = EF/e = VF
ZE/z' = VF/(Fz) = V/z >= 1 ⇔ V >= z = 1.5
と随分と単純になります。
また、節約される金額は、ケース4②よりF = (0.3r+0.8s+1.2) = 1.254とすると、
{(E/X)/10}*50 = 5E/(100z') = E/(20Fz) = E/{20*1.254*1.5} = E/37.62 ≒ 0.02658…E
zは一定なので、Eが大きくなればなるほど節約金額が大きくなります。
今回の場合、素材カードの基本獲得経験値の約2.66%だけ節約になります。
以上をまとめると、
常に金強化をする場合、
購入した素材カードが、購入額の1.5倍以上の獲得経験値を得られる場合は、
その素材カードは(消費銅銭的にも)お買い得です!
節約される金の総額は、購入した素材カードの獲得経験値の約2.66%です。
②素材を購入した場合にのみ、金強化
銅銭節約、という意味では①よりもこちらでしょうか。
ここまで抽象的な話が多かったので、一度具体的な例を見て考えてみましょう。
ケース3で紹介した、私が☆2極を1万で買った場合だとどうなるでしょう?
1万払って12000の経験値を得るわけですから、V = 1.2。
また、ケース5より、金強化を行う時のF = 1.254。
ケース3から、購入した素材カードの銅銭1当たりの獲得経験値の期待値ZEは、
ZE = FVz/(z-0.1V) = 1.254*1.2*1.5/(1.5-0.1*1.2) = 1.6356…≒1.64
これと、銅銭強化を行う時(F=1.04)のz' = 1.04*1.5 = 1.56を比較して、
ZE > z'
つまり、割とギリギリプラス^^;;
・・・というのを、以下で数式にします。
金強化時、銅銭強化時の合成結果補正をそれぞれF, F'とすると、上と同じく
ZE = FVz/(z-0.1V)
として、ZE > F'zとなればいいので、
ZE/(F'z) = FV/{(z-0.1V)F'} >= 1 ⇔ FV >= F'(z-0.1V)
これを整理して、
V >= {F'/(F+0.1F')}z = {1.04/(1.254+0.1*1.04)}*1.5 = 1.1487…z≒1.149z
購入素材でのみ金強化をする場合、
購入した素材カードが、購入額の約1.15倍以上の獲得経験値を得られる場合は、
金消費と対価に、その素材カードはお買い得です!
これだと、結構割に合うケースが増えてきますね^^
具体的な境界値は、上のまとめで貼ってある表をご参照の事。
随分な長文かつ、意味不明な解析記事に付き合って頂きありがとうございましたm(_ _)m







あけましておめでとうございます
返信削除ご無沙汰いたしております
今回はお役立ち記事ですね
筋金入りの文系である私としては
記事に数式があるだけで
(この人天才じゃん)
などと思ってしまいますが
今回もまた大変参考になりました
こういう記事はいいですね
もっともおバカな話(何気に失礼)も
読み物としては面白くて好きなのですが。
風邪が流行っております。お体ご自愛ください
あけおめことよろです~^^
削除こちらこそ、随分とご無沙汰しております><
こういう考察系ブログ、理屈っぽいIXAブログもすっかりなくなってしまい・・・
もうずいぶん遠くまで来たんだなと思ってしまう時がありますね。
月日は早いものです!
参考にして下さる人がいると、無駄に長々な記事を書いた甲斐が
あったというものですよ(笑
おバカな話はまぁ色々とスクリーンショットが貯まっているのですが・・・
もはや埋もれてきてしまい何処から書いていいものやらwww
天極を買ったり、色々売ったり、天スキル(!?)が付いたり、
知り合いの方に凸って悉くボコボコにされたり・・・
新年度までの忙しさの峠は越えたので、更新頻度はやや上がりそうですw
インフルエンザは年越し明けにやりましたし、
二度目は勘弁願いたいところです><;
寒い日が続きますが、鷹の団さんもご注意を~~ノ
あけおめ~!!
返信削除課金者には売っても二束三文だった武将の活用方法が見えてきてよかったです
あ、対戦の時はお手柔らかに
ことよろぉ~!!
削除ますます廃度に磨きがかかっておられるとお噂かねがね・・・
個人的には割と良アプデだと思います^^
各レアリティ、ランク毎に一定の価値を強化費用として担保して貰えると、
あまりにもゴミ価格過ぎた相場の是正につながる一助にもなるでしょうし・・・
カードの取引活性化もある程度は期待できるのではないかと思います。
しかし、以前にも増して銅銭が入手し難くなっていく一方で、
五右衛門や岡の効果は結局特に修正が入らず。
現状、銅銭スキルカードは全て排出停止ですし・・・
カード追加で壊れカードがこれからどんどん増えていく事を考えると、
限られた銅銭の投資先として、
やはり特定のカードのみが高騰する展開は避けられないでしょうか。。
絶対的な銅銭量増のために、ログインボーナスを頻発している所までは
私でもわかるのですが、カードインフレが急すぎて恩恵が薄いですね><w
インフレをもう少し押さえないと長期的な運営益にもつながらない
と考えるのですが・・・どうなのでしょう?
私の考えるイクサ、とか記事で語ると自分の底の浅さが知れてしまうので、
敢えて書きませんが(笑
こちらこそ宜しくお願いしますね―!
あけましておめでとうございます・・・でいいのかな
返信削除記事更新、ご苦労様です。
いつもながら、参考になる内容で助かります。早速、Lv上げに勤めます。
現在、東西戦準備期間中ですが、加勢がことごとく帰還の憂き目にあってまして、いつも以上に何もできずに終わりそうです。
乱筆乱文で申し訳ありませんが、今年もよろしくお願いします。
二カ月遅れなので・・・なんとも・・・言えないわけですが(笑
削除こちらこそ、今年も宜しくお願いします!
いえいえ・・・色々と合成結果などを教えて頂いたり、コメントを貰ったりしていながらブログ完全放置だったもので・・・申し訳なく・・・><w
東西戦、あっという間でしたねーw 濃縮された合戦と、言えなくも・・・